How many colors do you need to paint a map of the world? How should schools schedule final exams to minimize conflict for its students? How do you solve sudoku puzzles efficiently? Surprisingly, all of these questions are closely related mathematically. Namely, they are all questions regarding graph coloring.
What is graph coloring? To answer this, we must first establish what a graph is. In this context, a graph is a set of vertices connected by edges (1). Essentially, a graph is a network. Below is an example of a graph with 4 vertices and 6 edges:
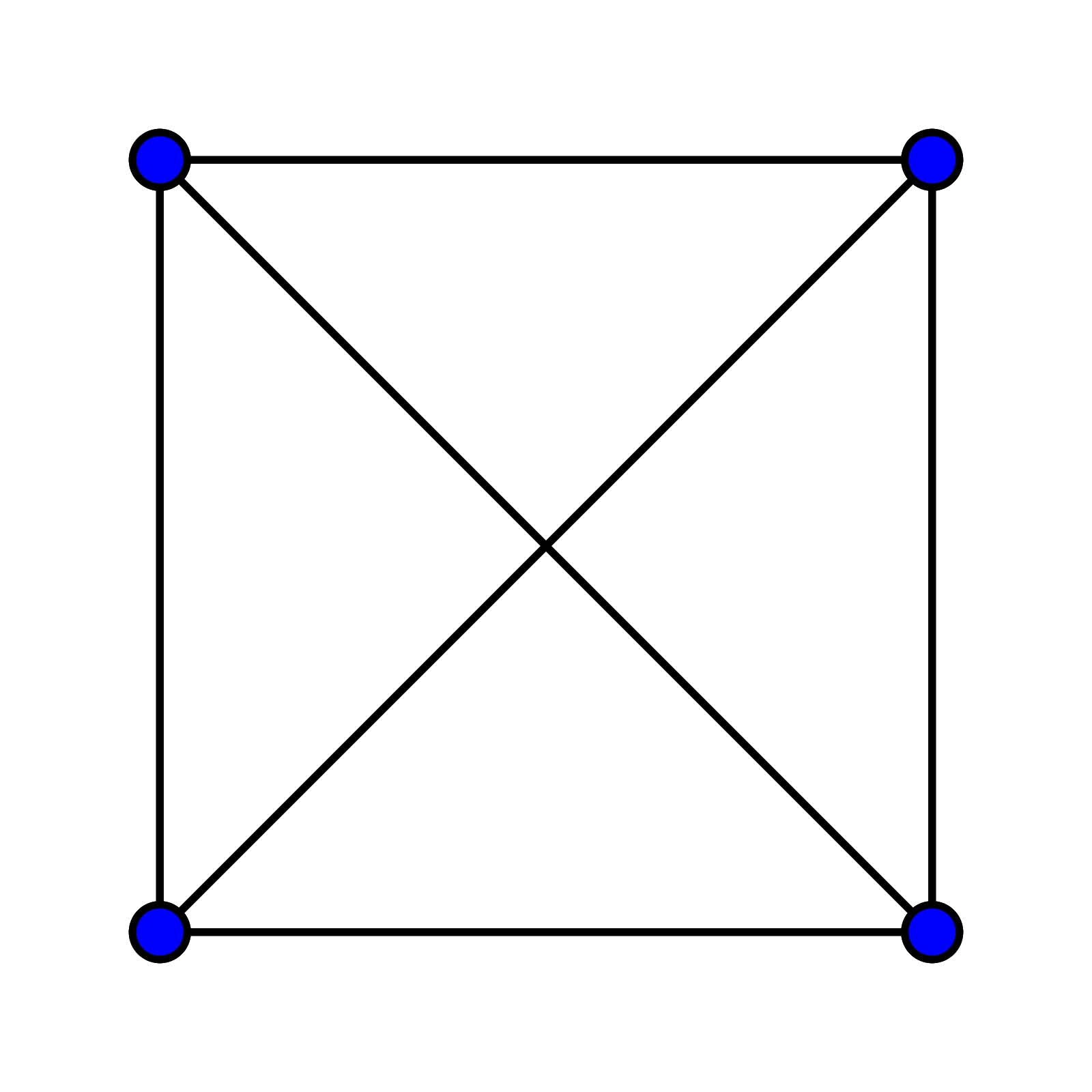
We say two vertices are adjacent if they are connected by an edge. In the example graph above, the 4 vertices are each adjacent to every other vertex. Graphs like these where each pair of vertices are adjacent are called complete graphs (1).
Vertex coloring is a special case of graph coloring when the vertices of a graph are colored such that no two adjacent vertices have the same color (2). Below is a graph with 11 vertices and 19 edges that can be colored using four colors:
With enough colors, any graph, no matter how complicated, can be colored. So, we are more interested in the smallest number of colors required to fully color a given graph G. This is called the chromatic number of graph G (1).
Now that we have discussed the most basic definitions of graph theory, we return to the question of painting a map of the world. Since we want to be able to tell the shape of each country clearly, any two countries that share a border should be painted using different colors. Since there are no restrictions other than this, this painting problem can be transformed into a vertex coloring problem. Namely, draw one point anywhere within the borders of each country and imagine drawing a “bridge” over every shared border on the map to connect the two points on either side. Then, the points in each country are the vertices and the “bridges” become the edges of this new graph that represents the map. Essentially, we have formed a graph by turning the countries into vertices and connecting two countries if they share a border. This way, painting a given map is the same as coloring the graph formed from it. We also know that any graph made from a map must be planar, which means that no two edges in the graph must cross each other. If the graph was not planar, then the borders would intersect on the map, and this is not possible. (3).
Thus, it suffices to find the chromatic number of planar graphs. It turns out that the chromatic number of any planar graph is four. The actual proof for this is much more complicated and involves using a computer to check many cases (4).
What about graphs that are not planar? Can they also always be colored with four colors? The answer, unfortunately, is no (5). In general, the question of finding the chromatic number of a graph is NP-complete, meaning that there are no quick and easy methods of solving it. While mathematicians Anuj Mehrotra and Michael A. Trick developed an algorithm for computing the chromatic number of small and medium sized graphs using a column generation approach (7), it does not solve the problem for all graphs (6).
Even though the vertex coloring problem is NP-complete, it still has many applications. As mentioned earlier, it can be applied to scheduling problems. This can be done by denoting the classes as vertices and connecting them if they share a common student. Then, the chromatic number is the minimum number of exam slots required to avoid any conflict exams. When solving Sudoku puzzles, one can represent each cell as a vertex and connect two vertices if the corresponding cells are in the same column, row, or three by three grid. Then, a valid graph coloring is equivalent to a solution of the Sudoku puzzle.
This article is intended to be a very basic introduction to graph coloring. Readers are urged to dive deeper into graph theory as it is both intuitive and applicable.
References:
- Adamchik, Victor. “Graph Theory.” School of Computer Science, Carnegie Mellon University , 2005, www.cs.cmu.edu/~adamchik/21-127/lectures/graphs_1_print.pdf.
- Guichard , David. “Graph Coloring.” Combinatorics and Graph Theory , Whitman College, www.whitman.edu/mathematics/cgt_online/book/section05.08.html.
- Walters, Mark. “It Appears That Four Colors Suffice: A Historical Overview of the Four-Color Theorem.” SIGMAA - History of Mathematics, Mathematical Association of America, 17 May 2004, historyofmathematics.org/wp-content/uploads/2013/09/2004-Walters.pdf.
- Weisstein, Eric W. "Four-Color Theorem." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/Four-ColorTheorem.html
- Graph Coloring and Chromatic Numbers. Brilliant.org. Retrieved 18:51, June 29, 2020, from https://brilliant.org/wiki/graph-coloring-and-chromatic-numbers/
- Weisstein, Eric W. "Chromatic Number." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/ChromaticNumber.html
- Mehrotra, Anuj, and Michael A. Trick. “A Column Generation Approach For Graph Coloring.” Carnegie Mellon University, 11 Apr. 1995.
